|
First of all, we look at Dekker's mutex algorithm, well known in the
literature. We will specify this algorithm in
CFA-format
(Communicating Finite Automata) which is one of
the modelling languages for the Kit.
In [RAY86] Dekker's mutex algorithm is described as
follows:
var flag: array[0..1] of boolean;
var turn: 0..1;
flag is initialized to false and turn has the value 0 or 1.
The protocol for process i then becomes:
flag[i] := true;
while flag[j] do if turn = j then
begin
flag[i] := false;
while turn = j do nothing enddo;
flag[i] := true;
end;
endif;
enddo;
[critical section];
turn := j;
flag[i] := false;
The next step is to create automata that specify the semantic behaviour
of each process. The corresponding automaton for process 1 is shown below.
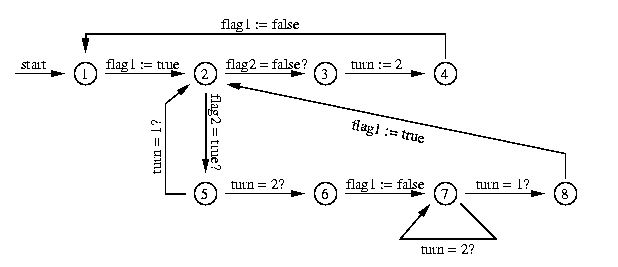
At this point we should say something about the labelling of the edges.
The symbol ':=' characterizes value assignment. For example, if the automaton
changes from state 1 to state 2, then afterwards the variable flag1 has
the value true. The expression variable=value? means a case of a
if-construct. So, if the automaton changes from state 2 to state 3,
then the variable flag2 had the value false before the execution
of this transition.
From this representation it is an easy task to derive the correct
specification of the algorithm in the CFA language.
The specification of the full system in the modelling language
CFA looks like the following:
CFA
@global
var flag1, flag2:{0..1} init 0;
var turn:{1..2} init 1;
| |
@automaton dek1 |
|
|
@automaton dek2 |
| |
A1 {@start @label "idle1"}. |
|
|
B1 {@start @label "idle2"}. |
| |
A2 {@label "trying1"}. |
|
|
B2 {@label "trying2"}. |
| |
A3 {@label "incs1"}. |
|
|
B3 {@label "incs2"}. |
| |
A5 {@label "trying1"}. |
|
|
B5 {@label "trying2"}. |
| |
A6 {@label "trying1"}. |
|
|
B6 {@label "trying2"}. |
| |
A7 {@label "trying1"}. |
|
|
B7 {@label "trying2"}. |
| |
A8 {@label "trying1"}. |
|
|
B8 {@label "trying2"}. |
| |
A1 [flag1'=1] A2 |
|
|
B1 [flag2'=1] B2 |
| |
A2 [flag2=0] A3 |
|
|
B2 [flag1=0] B3 |
| |
A3 [turn'=2] A4 |
|
|
B3 [turn'=1] B4 |
| |
A4 [flag1'=0] A1 |
|
|
B4 [flag2'=0] B1 |
| |
A2 [flag2=1] A5 |
|
|
B2 [flag1=1] B5 |
| |
A5 [turn=1] A2 |
|
|
B5 [turn=2] B2 |
| |
A5 [turn=2] A6 |
|
|
B5 [turn=1] B6 |
| |
A6 [flag1'=0] A7 |
|
|
B6 [flag2'=0] B7 |
| |
A7 [turn=2] A7 |
|
|
B7 [turn=1] B7 |
| |
A7 [turn=1] A8 |
|
|
B7 [turn=2] B8 |
| |
A8 [flag1'=1] A2 |
|
|
B8 [flag2'=1] B2 |
In the following we shortly describe the syntax we usdd.
Note that special keywords in our syntax are typed in boldface.
For more details see here.
First of all one must type the keyword CFA.
Then behind the keyword
@global one can define and initialize global variables.
The values in
braces denote the range of values of the variables. The specification of an
automaton begins behind the keyword @automaton.
dek1 and
dek2 are the names for the automata in our example. Now
the behaviour of the automata can be defined.
A1 and B1 are the entry states of
the automata as expressed by the keyword @start
typed in braces.
State identifiers can be extended with additional information like labels.
These informations can be written in braces behind the state identifier and
have the following format: keyword @label
followed by the label.
For example, the states A3 and B3 denote the critical regions in
the Dekker algorithm mentioned above and therefore we call them incs1
and incs2.
In this example, transitions from one state to another state are formulated
in two different ways: (for other possibilies see here)
A [x'=val] B (value assignment: x:=val)
A [x=val] B (test of equality)
where A and B are state identifier,
x is a variable and val a value.
For later use we write this specification to a file called
dekker.cfa.
Selected References
| [RAY86] |
|
| |
M. Raynal.
Algorithms for Mutual Exclusion.
North Oxford Academic Publishers Ltd, 1986. |
Next chapter: Checking a system for
deadlock-freeness
|

