This is a low level Petri net language intended to be used by machines. It is included in the Kit only because some tools can export models into this language. It is not intended as a modelling language for designing nets manually. For these reasons, we only describe the format shortly by means of an example. For full details of the PEP notation see here.

First we look at Dekker's mutex algorithm modelled as 1-safe Petri net:

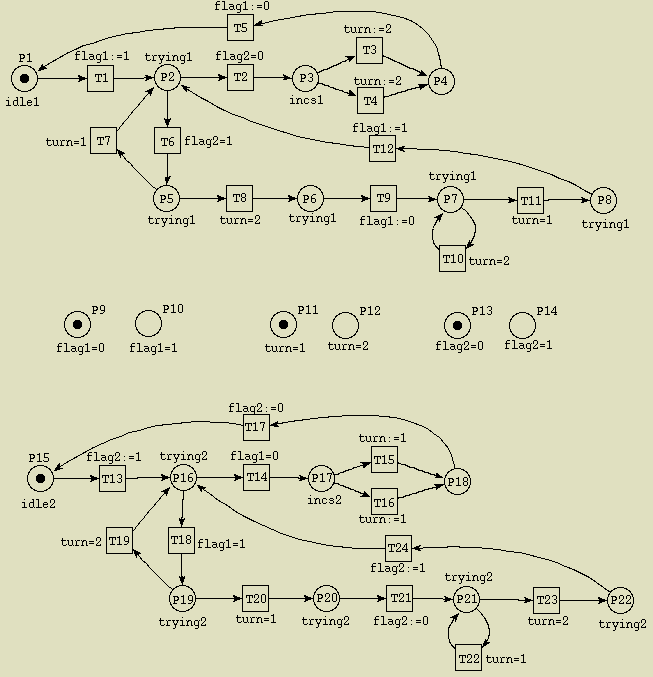
Places P9 through P14 denote different values of the variables. For example, if process 1 fires transition T1, then afterwards the value of variable flag1 should be set to 1. Moreover, we know that the value of flag1 is 0 before execution of T1. To model this behaviour correctly, we have to draw edges from P9 to T1 and from T1 to P10. Transition T2 should be fired only if process 1 stays in state P2 (it is marked) and if the value of variable flag2 is 0 before execution of T2. So we have to draw an edge from P13 to T2. Also, we must draw an edge from T2 to P13 because the value of flag2 will not be changed during execution of T2.

For the sake of clarity all edges connecting places P9 through P14 with transitions are omitted. See here for the Petri net with all edges.

In the PEP notation this Petri net looks like follows:

First, one has to define a header consisting of the keyword PEP, a keyword specifying the type of the LL-net (PTNet or PetriBox), and a keyword denoting the format (FORMAT_N or FORMAT_N2). Then, a list of all places must be given beginning with the keyword PL. For example, the line 1"P1"61@79b"idle1"M1m1 denotes a place with internal number 1. Its name is P1, and the coordinates for graphical representation are 61 and 79 (61@79). The place gets the meaning idle1 (b"idle1") and is initially marked (M1m1). Internal numbers and names of places must be unique. Behind the list of places one must define the list of transitions, beginning with the keyword TR. The transition definitions are followed by a list that specifies the arcs from transitions to places. The list begins with the keyword TP. For example, 6<6 denotes an arc from the transition with internal number 6 to the place with internal number 6. Lastly, one has to define the arcs from places to transitions. This can be done behind the keyword PT.

PEP
PTNet
FORMAT_N

% --------- Places ---------
PL

1"P1"61@79b"idle1"M1m1
2"P2"204@78b"trying1"
3"P3"342@79b"incs1"
4"P4"
5"P5"203@199b"trying1"
6"P6"347@199b"trying1"
7"P7"487@200b"trying1"
8"P8"640@201b"trying1"

25"P9"96@292b"flag1=0"M1m1
26"P10"209@291b"flag1=1"
27"P11"323@291b"turn=1"M1m1
30"P12"406@291b"turn=2"
28"P13"488@332b"flag2=0"M1m1
29"P14"586@331b"flag2=1"

23"P15"71@413b"idle2"M1m1
18"P16"214@412b"trying2"
19"P17"352@413b"incs2"
20"P18"
21"P19"213@533b"trying2"
22"P20"357@533b"trying2"
17"P21"497@534b"trying2"
24"P22"651@535b"trying2"

% --------- Transitions ---------
TR

1"T1"137@79b"flag1:=1"
2"T2"277@78b"flag2=0"
3"T3"406@51b"turn:=2"
34"T4"407@101b"turn:=2"
4"T5"277@28b"flag1:=0"
5"T6"204@141b"flag2=1"
10"T7"140@141b"turn=1"
6"T8"276@199b"turn=2"
7"T9"420@199b"flag1:=0"
11"T10"489@259b"turn=2"
8"T11"567@201b"turn=1"
9"T12"419@149b"flag1:=1"

32"T13"143@413b"flag2:=1"
33"T14"287@412b"flag1=0"
23"T15"415@394b"turn:=1"
35"T16"415@436b"turn:=1"
24"T17"287@362b"flag2:=0"
25"T18"212@475b"flag1=1"
30"T19"150@475b"turn=2"
27"T21"430@533b"flag2:=0"
26"T20"286@533b"turn=1"
31"T22"499@592b"turn=1"
28"T23"577@535b"turn=2"
29"T24"429@483b"flag2:=1"

% --------- Transition -> Place Arcs ---------
TP

6<6
6<30
7<7
7<25
11<7
11<30
8<8
8<27
9<2
9<26
32<29
32<18
33<25
33<19
23<20
23<27
35<20
35<27
24<28
24<23
25<21
25<26
30<18
30<30
2<28
2<3
3<4
3<30
34<4
34<30
27<28
27<17
26<27
26<22
1<2
1<26
31<27
31<17
28<24
28<30
29<29
29<18
4<25
4<1
5<29
5<5
10<2
10<27

% --------- Place -> Transition Arcs ---------
PT

20>24
21>30
21>26
22>27
1>1
2>5
2>2
3>3
3>34
4>4
5>6
5>10
6>7
7>11
7>8
8>9
25>33
25>1
25>9
17>28
17>31
24>29
26>7
26>4
26>25
27>8
27>35
27>31
27>3
27>26
27>10
30>6
30>23
30>11
30>28
30>34
30>30
28>29
28>2
28>32
29>24
29>5
29>27
23>32
18>33
18>25
19>23
19>35


Atomic propositions in formulae

Atomic propositions can consist of ...

• Place names
  A place name can be an atomic proposition, for example P1, P2, P3.
• Place meanings
  One can use the meaning of a place as atomic proposition, for example "incs1".

Meanings must be typed in quotes.